La cryptographie à courbes elliptiques

La cryptographie est omniprésente sur Internet. Sans elle, pas de sécurisation des connexions, et n’importe qui pourrait voir ce que l’on fait sur Internet.

Aujourd’hui la cryptographie recommandée est l’ECC (Elliptic Curve Cryptography), qui se base sur des fonctions mathématiques spéciales : les courbes elliptiques.

Qu’est ce qu’une courbe elliptique ?

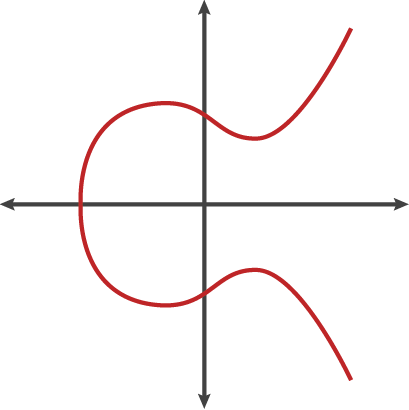Figure 1: Courbe elliptique ayant pour équation \(y^2 = x^3 - x + 1\) - Crédit : Cloudflare

Une courbe elliptique est une fonction mathématique particulière où :

• on choisit un point de départ sur la courbe, appelé point générateur \(G\) (donnée publique)
• on peut additionner des points entre eux selon des règles bien définies
• on peut répéter cette opération plusieurs fois (additionner un point avec lui-même)

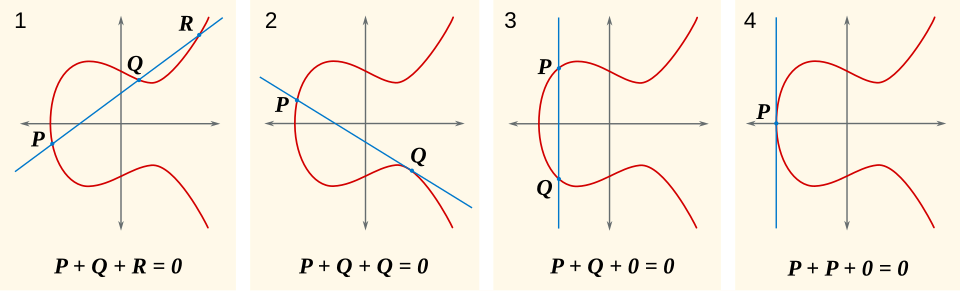Figure 2: Opérations possibles sur une courbe elliptique - Crédit : SuperManu, CC BY-SA 3.0 https://creativecommons.org/licenses/by-sa/3.0 , via Wikimedia Commons

Le plus intéressant dans ces courbes est le fait qu’il est très simple d’additioner des points, mais presque impossible de revenir en arrière.

Cette propriété est appelé le problème du logarithme discret sur les courbes elliptiques, et est la base de la sécurité de l’ECC.

Autrement dit, si on connait le point de départ et le résultat final, on ne peut pas savoir combien de fois l’opération a été faite.

Pourquoi utiliser les courbes elliptiques

Historiquement, pour sécuriser le trafic internet en HTTPS, le chiffrement RSA¹ était et est encore utilisé par soucis de compatibilité avec les systèmes plus anciens.

Cependant, les algorithmes basés sur les courbes elliptiques présentent plusieurs avantages majeurs :

• des clés beaucoup plus courtes pour un niveau de sécurité équivalent (par exemple, une clé ECC de 256 bits ≈ une clé RSA de 3072 bits)
• des calculs plus rapides
• moins de données échangées lors de l’établissement d’une connexion sécurisée
• une meilleure efficacité sur les systèmes contraints (mobiles, objets connectés)

C’est pourquoi les protocoles modernes (TLS, signatures numériques, cryptomonnaies, etc.) privilégient aujourd’hui l’utilisation de l’ECC.

Les signatures numériques

Les courbes elliptiques ne servent pas qu’au chiffrement : elles permettent aussi de signer des messages. C’est le principe de l’ECDSA (Elliptic Curve Digital Signature Algorithm).

Dans les cryptomonnaies, par exemple, ECDSA garantit qu’une transaction a bien été émise par son véritable propriétaire. Sans ce mécanisme, il serait possible d’usurper une identité et d’effectuer des transferts frauduleux.

Comme souvent en sécurité, la solidité du concept ne suffit pas : tout dépend aussi de la mise en œuvre. ECDSA repose sur un nombre aléatoire \(k\), différent à chaque signature. Si ce nombre est réutilisé ou mal généré, la clé privée peut être retrouvée à partir de seulement deux (2!) signatures.

Ce type d’erreur a déjà existé. Sur la PlayStation 3, par exemple, Sony utilisait un \(k\) statique dans son implémentation d’ECDSA. Des hackers ont alors pu retrouver la clé privée, ce qui a conduit au célèbre jailbreak permettant d’exécuter d’autres systèmes sur la console.

Lors de mes participations à des CTF, j’ai remarqué que je n’ai rencontré aucun challenge portant sur l’ECC… C’est pourquoi j’ai décidé, pour le CTF SecuRT 2026 (https://corslyn.github.io/projects/securt) , de réaliser un challenge où les personnes devront falsifier des signatures…

L’exploration de ce domaine de la cryptographie m’a permis de développer les Apprentissages Critiques (des sous-compétences permettant de valider des sous-compétences) du BUT Réseaux & Télécommunications. En particulier l’AC Choisir les outils cryptographiques adaptés au besoin fonctionnel du système d’information ainsi que l’AC Comprendre des documents techniques en anglais.